p?gebrd

Developer Reference for Intel® oneAPI Math Kernel Library for C

Download PDF

ID 766684

Date 11/07/2023

Version

Public

A newer version of this document is available. Customers should click here to go to the newest version.

Visible to Intel only — GUID: GUID-0FCEF7B7-6056-4427-892D-8E842BA6C443

View Details

p?gebrd

Reduces a general matrix to bidiagonal form.

Syntax

void psgebrd (MKL_INT *m , MKL_INT *n , float *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *d , float *e , float *tauq , float *taup , float *work , MKL_INT *lwork , MKL_INT *info );

void pdgebrd (MKL_INT *m , MKL_INT *n , double *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *d , double *e , double *tauq , double *taup , double *work , MKL_INT *lwork , MKL_INT *info );

void pcgebrd (MKL_INT *m , MKL_INT *n , MKL_Complex8 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , float *d , float *e , MKL_Complex8 *tauq , MKL_Complex8 *taup , MKL_Complex8 *work , MKL_INT *lwork , MKL_INT *info );

void pzgebrd (MKL_INT *m , MKL_INT *n , MKL_Complex16 *a , MKL_INT *ia , MKL_INT *ja , MKL_INT *desca , double *d , double *e , MKL_Complex16 *tauq , MKL_Complex16 *taup , MKL_Complex16 *work , MKL_INT *lwork , MKL_INT *info );

Include Files

mkl_scalapack.h

Description

The p?gebrd function reduces a real/complex general m-by-n distributed matrix sub(A)= A(ia:ia+m-1, ja:ja+n-1) to upper or lower bidiagonal form B by an orthogonal/unitary transformation:

Q'*sub(A)*P = B.

If m≥ n, B is upper bidiagonal; if m < n, B is lower bidiagonal.

Input Parameters

m

(global) The number of rows in the distributed matrix sub(A) (m≥0).

n

(global) The number of columns in the distributed matrix sub(A) (n≥0).

a

(local)

Real pointer into the local memory to an array of size lld_a*LOCc(ja+n-1). On entry, this array contains the distributed matrix sub (A).

ia, ja

(global) The row and column indices in the global matrix A indicating the first row and the first column of the submatrix A, respectively.

desca

(global and local) array of size dlen_. The array descriptor for the distributed matrix A.

work

(local)

Workspace array of size lwork.

lwork

(local or global) size of work, must be at least:

lwork≥nb*(mpa0 + nqa0+1)+ nqa0

where nb = mb_a = nb_a,

iroffa = mod(ia-1, nb),

icoffa = mod(ja-1, nb),

iarow = indxg2p(ia, nb, MYROW, rsrc_a, NPROW),

iacol = indxg2p (ja, nb, MYCOL, csrc_a, NPCOL),

mpa0 = numroc(m +iroffa, nb, MYROW, iarow, NPROW),

nqa0 = numroc(n +icoffa, nb, MYCOL, iacol, NPCOL),

NOTE:

mod(x,y) is the integer remainder of x/y.

indxg2p and numroc are ScaLAPACK tool functions; MYROW, MYCOL, NPROW and NPCOL can be determined by calling the function blacs_gridinfo.

If lwork = -1, then lwork is global input and a workspace query is assumed; the function only calculates the minimum and optimal size for all work arrays. Each of these values is returned in the first entry of the corresponding work array, and no error message is issued by pxerbla.

Output Parameters

a

On exit, if m≥n, the diagonal and the first superdiagonal of sub(A) are overwritten with the upper bidiagonal matrix B; the elements below the diagonal, with the array tauq, represent the orthogonal/unitary matrix Q as a product of elementary reflectors, and the elements above the first superdiagonal, with the array taup, represent the orthogonal matrix P as a product of elementary reflectors. If m < n, the diagonal and the first subdiagonal are overwritten with the lower bidiagonal matrix B; the elements below the first subdiagonal, with the array tauq, represent the orthogonal/unitary matrix Q as a product of elementary reflectors, and the elements above the diagonal, with the array taup, represent the orthogonal matrix P as a product of elementary reflectors. See Application Notes below.

d

(local)

Array of size LOCc(ja+min(m,n)-1) if m≥n and LOCr(ia+min(m,n)-1) otherwise. The distributed diagonal elements of the bidiagonal matrix B: d[i] = A(i+1,i+1), 0 ≤ i < size (d).

d is tied to the distributed matrix A.

e

(local)

Array of size LOCr(ia+min(m,n)-1) if m≥n; LOCc(ja+min(m,n)-2) otherwise. The distributed off-diagonal elements of the bidiagonal distributed matrix B:

If m≥n, e[i] = A(i+1,i+2) for i = 0,1,..., n-2; if m < n, e[i] = A(i+2,i+1) for i = 0,1,..., m-2. e is tied to the distributed matrix A.

tauq, taup

(local)

Arrays of size LOCc(ja+min(m,n)-1) for tauq and LOCr(ia+min(m,n)-1) for taup. Contain the scalar factors of the elementary reflectors that represent the orthogonal/unitary matrices Q and P, respectively. tauq and taup are tied to the distributed matrix A. See Application Notes below.

work[0]

On exit work[0] contains the minimum value of lwork required for optimum performance.

info

(global)

= 0: the execution is successful.

< 0: if the i-th argument is an array and the j-th entry, indexed j - 1, had an illegal value, then info = -(i*100+j); if the i-th argument is a scalar and had an illegal value, then info = -i.

Application Notes

The matrices Q and P are represented as products of elementary reflectors:

If m≥n,

Q = H(1)*H(2)*...*H(n), and P = G(1)*G(2)*...*G(n-1).

Each H(i) and G(i) has the form:

H(i)= i - tauq * v * v' and G(i) = i - taup*u*u'

where tauq and taup are real/complex scalars, and v and u are real/complex vectors;

v(1:i-1) = 0, v(i) = 1, and v(i+1:m) is stored on exit in A(ia+i:ia+m-1,ja+i-1);

u(1:i) = 0, u(i+1) = 1, and u(i+2:n) is stored on exit in A (ia+i-1,ja+i+1:ja+n-1);

tauq is stored in tauq[ja+i-2] and taup in taup[ia+i-2].

If m < n,

Q = H(1)*H(2)*...*H(m-1), and P = G(1)* G(2)*...* G(m)

Each H (i) and G(i) has the form:

H(i)= i-tauq*v*v' and G(i)= i-taup*u*u'

here tauq and taup are real/complex scalars, and v and u are real/complex vectors;

v(1:i) = 0, v(i+1) = 1, and v(i+2:m) is stored on exit in A (ia+i:ia+m-1,ja+i-1); u(1:i-1) = 0, u(i) = 1, and u(i+1:n) is stored on exit in A(ia+i-1,ja+i+1:ja+n-1);

tauq is stored in tauq[ja+i-2] and taup in taup[ia+i-2].

The contents of sub(A) on exit are illustrated by the following examples:

m = 6 and n = 5(m > n):

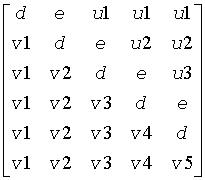
m = 5 and n = 6(m < n):

where d and e denote diagonal and off-diagonal elements of B, vi denotes an element of the vector defining H(i), and ui an element of the vector defining G(i).

Parent topic: Singular Value Decomposition: ScaLAPACK Driver Routines

Select Your Language

Using Intel.com Search

Quick Links

Recent Searches

Advanced Search

Only search in

Developer Reference for Intel® oneAPI Math Kernel Library for C

p?gebrd

Syntax

Include Files

Description

Input Parameters

Output Parameters

Application Notes

See Also